Dimensionality reduction is a technique employed in machine learning and data analysis to condense large datasets while preserving the most significant information. Modern datasets often contain hundreds or even thousands of features.
Working with such high dimensional data can slow down algorithms, increase storage needs, and make patterns harder to detect. Learning these concepts is an essential part of any Artificial Intelligence Course in Mumbai at FITA Academy, where students gain hands-on experience in managing complex datasets. Dimensionality reduction helps solve these challenges by creating a smaller and more manageable representation of the data.
Why Dimensionality Reduction Matters
High dimensional data can introduce noise, redundancy, and unnecessary complexity. Many features may not contribute meaningful insights and can confuse models. By reducing the number of features, analysts can improve training speed, enhance visualization, and prevent models from overfitting. Dimensionality reduction also helps reveal hidden structures inside the data that would otherwise remain difficult to observe.
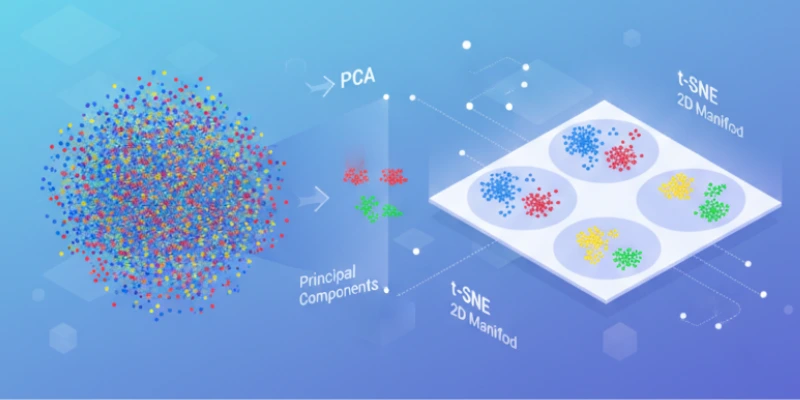
Two of the most widely used techniques for dimensionality reduction are Principal Component Analysis and t Distributed Stochastic Neighbor Embedding. Every approach has its own purpose and is most effective in particular circumstances.
Studying at a B School in Chennai equips students with practical knowledge of advanced data analysis techniques such as dimensionality reduction. This skill helps in efficiently handling large datasets and extracting insights that are valuable for strategic decision-making.
What is Principal Component Analysis
Principal Component Analysis, also known as PCA, is a statistical technique used to convert a large set of variables into a smaller set of new variables called principal components. These components represent directions of maximum variance in the data. In simpler terms, PCA finds patterns by identifying how the data varies most strongly.
PCA is a linear method. It works well when the relationships within the data follow straight line patterns. It is often used to speed up machine learning models, reduce noise, and create cleaner visual representations. Learners enrolled in an AI Course in Kolkata can learn how to apply PCA effectively on real-world datasets. Since PCA keeps the directions that capture the most variance, it helps preserve the overall structure of the data while discarding weaker signals.
What is t-SNE
t Distributed Stochastic Neighbor Embedding, or t-SNE, is a nonlinear technique designed primarily for visualization. Unlike PCA, t-SNE focuses on preserving local relationships within the data. It examines how similar points cluster together and attempts to represent those clusters clearly in a lower dimensional space. This makes it especially useful for complex datasets such as image embeddings, high dimensional vectors, or data with curved and layered structures.
t-SNE creates detailed two dimensional or three dimensional maps that reveal natural groupings. These maps are often easier for humans to interpret. Although t-SNE is powerful, it is more resource intensive and less suitable for general dimensionality reduction tasks used for model training.
When to Use PCA and When to Use t-SNE
PCA is a strong choice when working with large datasets that need quick and efficient feature reduction. It performs well when the data shows mostly linear patterns. On the other hand, t-SNE is ideal when the goal is to explore and visualize complex relationships. It highlights subtle clusters that PCA might miss. Joining AI Courses in Delhi can help gain hands-on experience with both PCA and t-SNE, preparing them to handle large and complex datasets effectively.
Both methods play an important role in modern data analysis. Understanding how and when to use them helps create clearer insights, faster models, and more meaningful interpretations.
Also check: Neural Networks How They Mimic The Human Brain




Recent Comments